
Simplification de surface dépendante du point de vue.
Projet de DEA : L'objectif de ce projet est de développer un algorithme pour optimiser le calcul de l'attraction gravitationnelle des reliefs. Pour calculer l'attraction d'un volume délimité par une surface triangulée, il faut intégrer sur toute les facettes une fonction*. Le but du stage est de simplifier la surface triangulée sur laquelle on travaille, en fonction de la distance à un point ( le point de calcul). Ce stage est mon projet de DEA Image, Vision et Robotique. Il a eu lieu à l'IGN ( Institut National de Géographie, équipe LAREG).
(*) : l'attraction d'un volume se calcule par une intégrale sur le volume, mais grâce au Théorème de Gauss, on peut la transformer en intégrale sur la surface. Il suffit donc d'intégrer sur chaque triangle et de faire la somme de toutes les composantes. Dans notre cas, on retransforme encore l'intégrale sur un triangle en intégrale sur les segments du triangle, toujours avec le Théorème de Gauss.
ALGORITHME
L'algorithme est séparé en quatre parties :
Triangulation
d'un MNT ( Modèle Numérique de Terrain)
régulier :
Le mnt est une grille régulière contenant des
altitudes. On lit donc ces altitudes et triangule la surface
équivalente. Il faut aussi trianguler la surface d'altitude
0 ( surface sphérique ) et aussi les bords du mnt pour
fermer le volume. Pour 4 points, on a deux possibilités pour
construire les deux triangles associés. On a alors
développé deux méthodes : on peut
trianguler toujours de la même façon ou bien
choisir la configuration qui approche au mieux une interpolation Spline
( Catmull-Rom ) des 16 points aux alentours.
Simplification
de la surface avec construction de la liste de "edge-collapse" :
On va ensuite simplifier la surface construite. Les algorithmes de
simplification de surface sont nombreux. Après
étude, on a choisi celui de Lindstrom & Turk car il
conserve le volume défini par la surface. Or dans notre cas
précis, c'est précisément une erreur
de volume qui entraîne une erreur sur l'attraction
gravitationnelle. De plus, cet algorithme est disponible en OpenSource
dans la librairie GTS ( Gnu Triangulated Surface), ce qui au vu de la
durée du stage est important.
voir "Progressive
meshes. H. Hoppe. ACM SIGGRAPH 1996, 99-108."
pour la construction des edges-collapses successifs.
voir "Fast
and Memory Efficient Polygonal Simplification. Peter
Lindstrom and Greg Turk. IEEE Visualization '98, October 1998, pp.
279-286, 544." pour l'algorithme de simplification de surface.
Il aurait été intéressant
d'étudier l'erreur causé par le
célèbre algorithme de simplification de surface
de Garland et Eckbert ( voir M.
Garland and P. Heckbert. Surface Simplification Using Quadric Error
Metrics. In Proceedings of SIGGRAPH 97 ).
Construction
de la simplification hiérarchique :
Il faut ensuite adapter la simplification construite pour que les
triangles soient nombreux et précis proche du point de
calcul et plus grossier loin du point de calcul. Pour cela, on commence
par mémoriser toutes les arrêtes
simplifiées. On mémorise ainsi une
séquence de "edge-collapse". On construit ensuite un arbre
de ces "collapses" qui permet de choisir quelles simplification on veut
faire ( par exemple celles loin du point de calcul).
voir "Smooth
view-dependent level-of-detail control and its application to terrain
rendering. H. Hoppe. IEEE Visualization 1998, October 1998, 35-42."
Boucle
de calcul
On peut alors exécuter la boucle principale, c'est
à dire simplifier la surface pour le point ou l'on
exécute le calcul, exécuter le calcul. Changer le
point de calcul, re-simplifier pour ce point et refaire le calcul...
ainsi de suite pour tous les points de calcul. L'algorithme optimise le
changement du point de calcul si le suivant est proche de l'actuel.
ILLUSTRATIONS

l'interface pour visualiser les MNT. ( vue du bord da la zone étudiée)
|
|
surface initiale à 500.000 segments |  |
simplifiée à 9000 segments | |
 |
simplifiée à 1000 segment |  |
simplifiée à 150 segments | |
 |
simplification extrême à 37 segments | |||
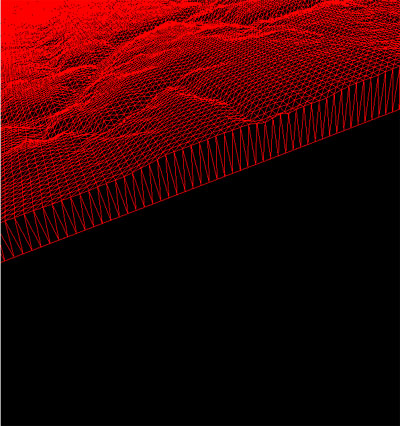 |
Une zone de relief, avec vallées et plateaux qui va être simplifiée. |  |
On vérifie que les endroits simplifiés sont bien les plateaux. Les zones de courbures comme les vallées conservent beaucoup de triangles. | |
 |
exemple de simplification lorsque le point de calcul est en bas à gauche. |  |
encore pus simplifié | |
 |
encore un peu |  |
simplification extrême | |
 |
sur cette simplification, la qualité des triangles diminuent doucement quand on s'éloigne du point de calcul. |
|
Ici, la qualité diminue très vite après un seuil. Il faut tester pour mesurer l'impact sur la précision du calcul de gravité. |
ASPECT LOGICIEL
Tous les développements ont été réalisés en C++, sous Linux avec l'IDE KDevelop 3.0, le compilateur gcc, le générateur de doc Doxygen, les outils GNU autoconf, libtool et automake.
Tout d'abord, pour bien vérifier la lecture correcte du MNT, ainsi que pour valider la triangulation construite, j'ai décidé de développer un logiciel de visualisation 3D adapté. Le logiciel permet de charger un mnt et de visualiser la surface associée. On peut ensuite simplifier la surface selon un point, faire bouger le point selon une boucle et ainsi visualiser la simplification adaptative. On peut fixer les paramètres des algorithmes, afficher des informations sur l'état des structures de données. L'interface est réalisée sous QT, le widget de visualisation 3D est un objet de la librairie Coin3d ( identique à OpenInventor). Cela permet de développer très rapidement un outil pour visualiser et manipuler des données 3D.
Pour le programme de calcul de l'attraction gravitationelle, j'ai repris le code existant développé par mon tuteur, qui permet de calculer l'attraction d'un volume délimité par une surface triangulée. J'ai ensuite ajouté la simplification de surface dépendante du point de calcul ( pris dans la librairie GTS ).
J'ai aussi développé de nombreux petits exécutables annexes pour manipuler les mnt, en extraire une partie, changer leur format et aussi des scripts shell pour lancer les tests avec divers paramètres.
Author : Adrien
Auclair
adrien.auclair at club-internet.fr
Last update : 16/07/2004