
View-point dependant surface simplification.
Master thesis project : Goal of this project is to compute the gravitationnal attraction of large volumes (i.e. mountains). The definition of the gravitationall attraction is given by an integration over a volume. Using the Gauss theorem, one can reduce it on an integration over a surface. By simplifying the surface (number of triangles), our idea is to decrease the computation time. In order to keep a desirable level of precision, surface must be simplified far from the computation point and must be as precise as possible close to this point. Because the computation is usually computed over a whole map (a grid of points), the surface simplified for one point must be fastly adapted to its neighbor computing point.
This project was achieved as a master thesis (Master of research in Image, Vision and Robotics, INPG University, Grenoble). It was supervised by Olivier Jamet, LAREG team, at the National Institute of Geography.
ALGORITHM
Algorithm is split in four parts :
regular
MNE Triangulation (numerical Model of Elevation given on a regular
grid) :
MNE is a regular grid where elevation is given at each node. The
surface is triangulated from these elevation values. The surface at
elevation 0 is also triangulated, as are the sides of the given area.
Eventualy one obtain a closed triangulated surface. In this thesis, I
studied the influence of the choice of the triangulation (regular of
using a Catmull-Rom spline).
Surface
simplification and creation of a list of "edge-collapse":
There exists many surface simplification algorithm. We decided to use
the one of Lindstrom & Turk because it doesn't modify the
volume
encapsulated in the closed surface. And in our case, the error would
lead to error in the computation of the gravitationnal attraction. And
this algorithm is freely available in the GTS library (Gnu Triangulated
Surface).
see "Progressive
meshes. H. Hoppe. ACM SIGGRAPH 1996, 99-108."
for the building of "edge-collapse" list..
see "Fast
and Memory Efficient Polygonal Simplification. Peter
Lindstrom and Greg Turk. IEEE Visualization '98, October 1998, pp.
279-286, 544." for the surface simplification algorithm.
That would also hae been interesting to study the error
caused by the famous simplication surface algorithm : M.
Garland and P. Heckbert. Surface Simplification Using Quadric Error
Metrics. In Proceedings of SIGGRAPH 97 ).
Hierarchical
surface simplification :
Next step is to adapt the surface depending of the computation point.
Surface must be much simplified far away and keep much precision close
to this point. This is achieved using the hierarchical descipription of
the previous surface simplifaiction, see "Smooth
view-dependent level-of-detail control and its application to terrain
rendering. H. Hoppe. IEEE Visualization 1998, October 1998, 35-42."
Computation
loop
Once the hierarchical surface representation is created, one can enter
in the main loop. The surface is simplified for a point, then
computaion is done at this point. Then, surface is slightly adapted for
a neighboring computation point. This is a quick step, thanks to the
hierachical representation. Computation can be laucnhed again at this
point, and so on.
ILLUSTRATIONS

the UI to visualize the MNE (side of the studied are)
|
|
initial surface :500.000 edges |  |
simplified to 9000 edges | |
 |
simplified to 1000 edges |  |
simplified to 150 edges | |
 |
simplified to 37 edges | |||
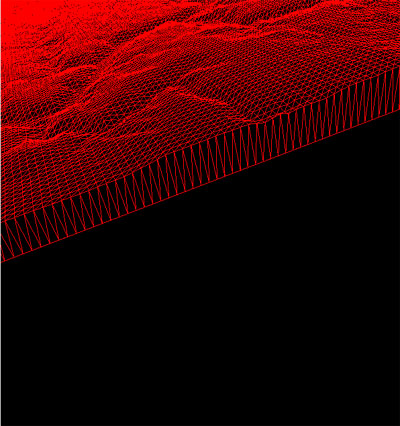 |
An area with mountain and flat parts. |  |
The flat parts are simplified first | |
 |
Example of a simplification, the computaion point is in the low-left corner. |  |
Same point, but more simplified | |
 |
more simplification |  |
extremal simplification | |
 |
On this simplification, the quality of the mesh decreases slowly as one gets further from the computation point |
|
Here, the decrease of quality if very steep. |
Author : Adrien
Auclair
adrien dot auclair at gmail dot com
Last update : 16/07/2004