
| Metaballs 3D |  |
Les metaballs 3D sont le prolongement de l'effet 2D mais en 3D. L'effet peut donner des résultats superbes, même si la version proposée ici est assez basique. Le principe sert aussi dans certains modeleurs 3D pour dessiner des surfaces qui se mélange sous un aspect visqueux. On retrouve l'effet dans l'intro de Colin McRae chez CodeMasters.
Principe :
Selon le même principe qu'en 2D, une metaball génère un potentiel proche d'elle, par exemple un fonction du style cos(d/D_MAX*PI/2) où d est la distance au centre de la metaball, mais cette fois-ci dans l'espace 3D.
Il suffit ensuite de sommer les effets de toutes les metaballs pour obtenir une matrice 3D des potentiels. On affiche ensuite une unique isosurface. Une telle surface représente un lieu ou le potentiel est constant ( équivalent d'un ligne de niveau en 2D ). La partie complexe est donc d'extraire à partir d'une grille 3D de valeurs une iso-surface. Pour cela, on utilise le célèbre algorithme de marching-cube. Ce dernier parcours tous les cubes de la grille de valeurs et pour chacun crée les triangles de l'isosurface s'ils existent.
marching-cube :
on trouve de nombreux articles à son propos tellement cet algorithme est utilisé, et cela dans de nombreux domaines : graphisme, imagerie médicale, prospection du sous-sol... Son principe de base est très simple. Par exemple, on veut trouver les triangles de l'isosurface pour un seuil donné s. Pour chaque cube de la matrice 3D, si un sommet a un potentiel supérieur à s, il est INSIDE, si son potentiel est inférieur à s, il est OUTSIDE. Pour 8 sommets, cela fait 256 configurations possibles pour un cube. Mais par symétrie, on retombe en fait toujours sur l'une des 15 configurations suivantes :
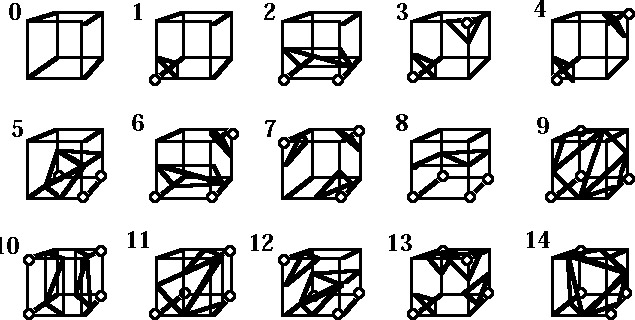
Ce schéma nous donne les triangles à afficher pour dessiner l'isosurface pour un cube donné. Un cercle sur un sommet indique qu'il est INSIDE, sinon, il est OUTSIDE. L'algo parcout donc tous les cubes de la grille 3D, pour chacun, il cherche la configuration associée, et affiche les triangles de cette configuration. Pas comliqué. Ensuite, on fait bouger les metaballs, et on recommence...
Optimisation :
En fait, on ne parcours pas tous les cubes de la matrice 3D lors du marching-cube, cela serait trop long. On utilise le fait que lorsqu'un cube fait partie de l'isosurface, ses voisins en font certainement partie. Pour être certain d'avoir toutes les composantes de l'isosurface ( qui peut comporter plusieurs composantes déconnectées), on fait un lancer de rayon depuis chaque metaball à la recherche d'une intersection avec l'isosurface.
fichier téléchargeable : metaballs3D.tar ( 60 kb) ( source+makefile Linux)
Le fichier .tar à télécharger contient le source et un makefile Linux ( nécessite OpenGL et glut )
| |
|
||
| |
|
||
| en vert : la matrice des valeurs | |||
| |
|
||
| en vert : la matrice des valeurs | |||
| |
|
Author : Adrien
Auclair
adrien.auclair at club-internet.fr
Last update : 16/07/2004