Metaballs 3D

3D Metaballs are an evolution of the principle of 2D metaballs. The effect can give beautiful results. The version explained here just explains the basic of the effect. A very nice version was used in the intro of Colin McRae from Codemasters.

Then, the 3d potential map  is computed by adding the potential of each metaball. From this 3D grid of scalar values, we need to extract a surface (a mesh). We need to choose a threshold s. All the values greater than s will be inside the surface (because large potential means close to metaballs centers). All the values smaller than s will be outside the surface. So we need to extract the surface where the potential is s. This is called an isosurface. The algorithm to extract such surface is called a marching-cube. 

This algo is used has many applications : modeling, medical apps...  Its principle is to walk through all the cubes of the 3D grid of data. And for each cube, it tells which triangles to create. For a given cube, each vertex can have a potential larger or smaller of the threshold s. So with 8 vertices, that leads to 256 possible configurations for a cube. Using symmetry, there are in fact only 15 different configurations. In the following pictures, these configurations are displayed. A vertex with a circle on it means it is inside the surface (potential larger than s).

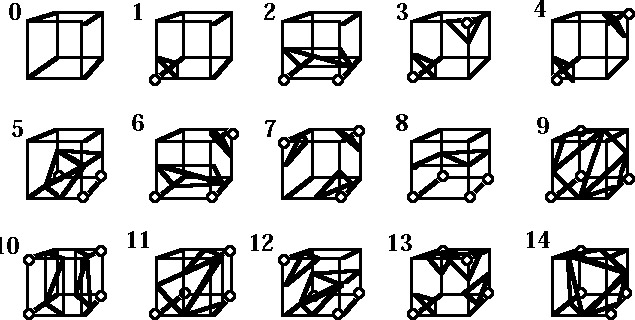
Knowing the traingles of the surface for each cube, we just have to display them. Then we loop (move the metaballs compute everything again).

In fact, that would be too slow to walk over all the cubes. We use the fact that is a cube contains triangles of the isosurfaces, its neighbors could also contains some. So we start by searching  a first cube with triangles (config different of 0), then we only walk iteratively through the neighboring cubes. To be sure to get all the components of the isosurface, I trace a ray ( in the 3d grid) from each metaball centers to look for the intersection of the isosurface.

Download

file : metaballs3D.tar ( 60 kb) ( source+makefile Linux)

The .tar file contains the source code and a Linux makefile  (needing openGL and glut)

Screenshots Gallery

			in green, the matrix of values (the grid)
	in green, the matrix of values (the grid)

Author :  Adrien Auclair  
adrien.auclair at club-internet.fr
Last update : 16/07/2004